接續昨天的文章，今天要介紹的是 flow-based model 如何估計真實影像的機率分布，而這部分內容會用到一些線性代數和微積分的概念或定理，還不瞭解的話可以先參考前一篇文[Day 14] Flow-based model 的數學原理（一）～

首先回顧一下 flow-based model 生成影像的過程：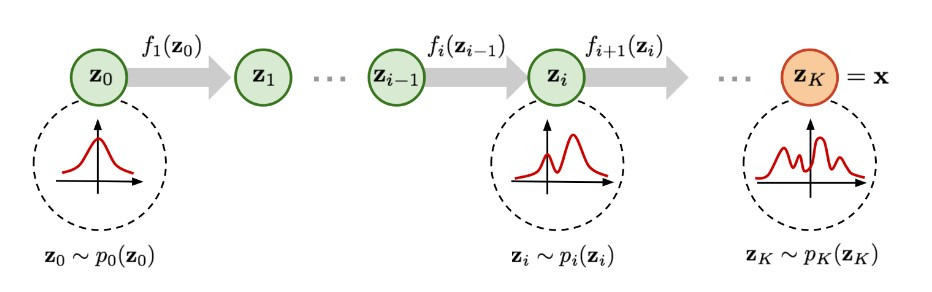

（圖片來源：Flow-based Deep Generative Models | Lilian Weng）

如同其他生成影像的過程，一開始都會從常態分布（或其他較簡單的分布）抽樣得到 code 向量 z0，通過模型最終產生影像 x。不過 flow-based model 由於限制 generator 必須是可逆函數（如此才能計算得到影像分布 p(x)，會讓單個 generator 產生影像的能力受限，因此必須串接多個 generator 才能達到比較好的影像效果。

因此 flow-based model 詳細的生成影像過程會是：常態分布抽樣得到的 code 向量 z0 通過第一個 generator f1 得到中間向量 z1，z1 所屬的分布會比常態分布更複雜一點。而 z1 會再通過下一個 generator f2，得到 z2，z2 的分布又會比 z1 的分布更複雜。以此類推，直到通過 K 個 generator 得到影像 x，假設這 K 個 generators 接在一起有足夠的學習能力，我們就能將 code 分布一步一步轉換到近似真實影像的分布。

根據昨天介紹的內容，當我們用 p(x) 代表影像的分布， π(z) 代表 code 的分布，G(z) 為 generator，其反函數 G^-1(x) 為 encoder，我們可以這樣表示影像分布 p(x)：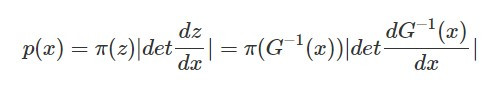

依照今天解釋的生成影像過程調整一下式子裡的表示符號，我們可以得到第 i 個分布 p_i(z_i) 的表示式：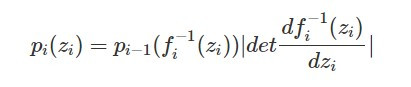

根據反函數定理，我們可以將上面的式子整理成從第 i-1 的分布 p_(i-1)(z_(i-1))轉換到第 i 個分布 p_i(z_i) 的關係式：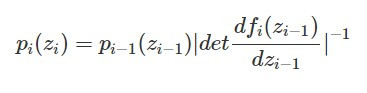

等號兩邊取 log 可以得到：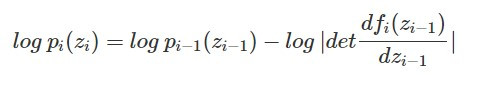

而在串接 K 個 generator 時，我們可以依照上面的式子一步一步回推 code 分布 p_0(z_0) 與影像分布 p_K(x) 的關係：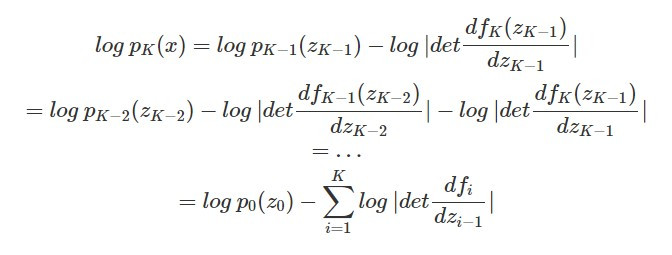

在訓練生成模型時，都是希望模型能學到一組參數讓學到的分布和真實影像的分布越接近越好，換句話說就是在給定一些真實影像資料 x_i 的情況下，最大化（模型學到的）生成分布能產生這些資料的可能性（likelihood），可以表示如下：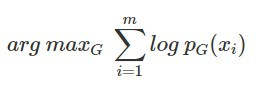

由於我們可以明確的用數學式子表示 flow-based model 的生成分布，因此可以直接以上式作為模型的學習目標，用 maximum likelihood estimation 的方式得到模型的參數。

值得注意的是，VAE 由於缺乏對模型架構的限制，無法直接最大化 likelihood，而是推算得到 likelihood 的 lower bound 作為模型學習的目標。因此從原理來看，flow-based model 更直接的達成和真實分布接近的目標～